Anton's Research Ramblings

Interpolation Functions aka "Tweening" or "Easing"

In visualisation and games we often have animated transitions of visual elements. This could be an actor walking between two points, or a menu button moving into place, or a perhaps chart transitioning to a new data set. Most of the transition animations are fluff - they provide no intrinsic value whatsoever, but appear pleasing to the user/audience. And there is value in that, lots of value. Arguably these transitions are more important to animations which only store "key frames" and expect real-time animation to interpolate between these as required. On St Patrick's Day holiday I spent some time looking into this and making my own interpolation library.

There is a lot of dubious-quality literature around on this topic, which very much reads like a bad re-invention of really basic mathematical functions. A quick google on "easing functions" or "tweening" [cringe] will give you a slice of this. There are some nice, animated, examples at easings.net. I wanted to use some similar functions in my own projects to add some glitter value, but I immediately found some problems with the available resources:

• A non-standard notation convention for variables is used, which I find confusing.
• Basic mathematical functions like exponentials tend to be crudely approximated with staggered if-else statements, as if the writer didn't know how to make a simple quadratic or exponential function.
• Code in commonly-used libraries would generate in-efficient machine code, is hard to read, and is of a generally poor standard.
• Functions all proceed in one direction, but are named "in" and "out" instead of an accurate analogy such as "accelerating" and "decelerating".
• Functions are "impure" in that they have fixed-sized lead-ins to wave functions tied to the same scale - this seems flat out dumb. Why not use two separate functions for the lead-in and wobble?
• Most of the non-linear transition functions in the "easing" functions are so similar when viewed in one dimension that you couldn't tell the difference without looking at a 2d chart.

With these considerations I decided to just make my own little collection of interpolation functions. I immediately threw out most of the package of "easing" functions, and only implemented the few that I thought would provide obvious and interesting transitions. Rather than copy the common functions from some library, I just approximated them with as simple as possible pure maths functions, and as little logic as possible. I replaced all the unusual input parameters with current x, initial x, final x, initial y, and final y, the way we would define these things in my mechanics education.

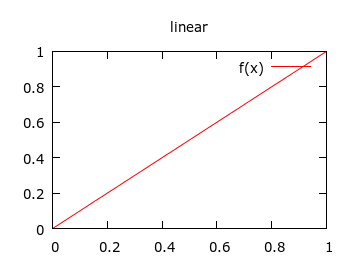
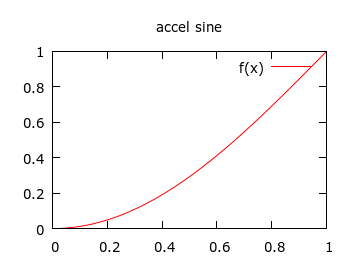
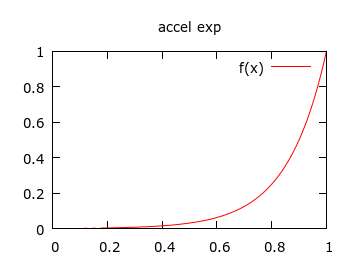
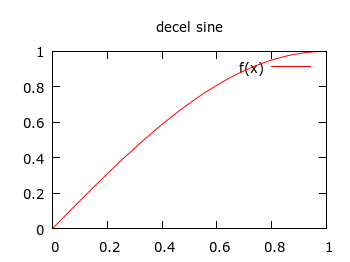
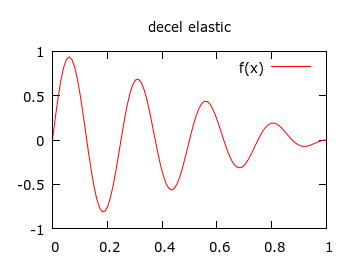
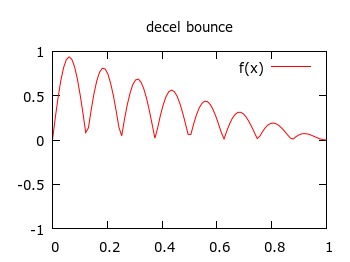
I started with the above, simple functions, which are pretty similar to the "easing" set, and modelled them in gnuplot to see if they looked okay. Then I smashed them into some simple C functions with my basic parameters. The code is available on GitHub. I tried it out for a title animation in my Crongdor the Barbarian game, and it looked pretty good. I wanted the title to drop down, and then bounce, as if hitting a surface. Rather than use a fixed-size lead-in, as in the easing functions, I just did an exponential interpolation (like gravity) between start height, and end height, then a bounce interpolation, which for me is like a linearly diminishing absolute sine wave.