[index]
Anton's Research Ramblings
Debunking 'Gimbal Lock'
The Two Types of Maths Chapter
When you read texts on 3d graphics you always get to what writers call the
'dreaded maths chapter'. I don't like this. As a pragmatist, I was never
stimulated by pure maths and calculus, but found myself learning it later when
it started to become genuinely useful for engineering and computer graphics
applications. Writers in computer graphics texts tend to fall into two
categories:
- Massively theoretical; providing extended proofs, with little or no
discussion, leaning on other mathematical concepts that the reader may not
have encountered before.
- Overly familiar and chummy, somewhat patronising the reader not to be
'scared' of the maths chapter, and brushing all of the details under the
carpet.
The first approach only appeals to those with a pure mathematics background, or
perhaps, more accurately - the narrow band of personality types to which that
appeals. I don't like this because it cuts out 3/4 of a class from progressing,
even though they are capable of understanding the material if presented
differently. There is a certain level of elitism amongst computer scientists,
who would more than happily pooh-pooh any students not up to that level...which
would be fine if modern computer science programmes actually re-enforced
calculus, and science fundamentals - which they don't. These days computer
science degrees are basically glorified IT vocational training with very little
depth at the undergraduate level, and expecting even fourth-level students to
have this knowledge when they finally get to the graphics class is kind of
uncool. It's actually not hard to learn the mathematics required for 3d
transformations - I suspect even the most efficient way to learn because you
have real tangible visual rewards when it goes correctly. I got a lot of
traction from finding practical, hands-on ways to explain these concepts to
students - the same way that it appealed to me. Now, that's not my only problem
with approach number 1. Some very popular texts in the field tend to
dump pages of proofs that don't always seem to be terribly applicable to the
problems at hand - the "dazzle them with maths" approach to hide the gaps in
the writer's knowledge.
The problem with the second approach is that, even at the expert level, writers
in games and graphics often have a very poor grasp of the mathematics
themselves, and lean on analogies instead of stepping breaking down and stepping
through the problem logically. This is a bunch of nonsense. Enter: 'Gimbal
Lock'.
Frightening Students
One of the most terrifying mathematical concepts to pop-up to graphics students
is a concept used for rotation - Hamilton's quaternions. At some point, the
student will get their head around matrix rotation, and will try to make either
a free-moving 3d camera, or some sort of space-ship game, or a vehicle moving
on slopes. It gets really hard to work out by combining fixed-axis X,Y, and Z
rotation matrices. What you really want to is to derive a local X, Y, and Z
axis, and perform a local (from the point of view of the object or camera being
rotated) pitch/yaw/roll instead.
Typically, the student will try to combine a series of X, Y, and Z rotations.
It will sort-of work, in some ranges of orientation, but come unstuck when you
really need 3 axes to rotate at once. You can change the order around, but then
it won't work in the original ranges of angle. If you open any graphics or
games maths textbook you'll come to the Quaternions section, and get one of the
two styles of explanation, as discussed above. If you're a pragmatic person,
you're not going to be satisfied by either of them. Firstly, the proofs don't
give you the practical functions that you're looking for, and raise more
questions than they answer. You may even get a diagram in 2d explaining how a
hypersphere in 4d expresses rotation, pulsating in size as the angle changes.
The inter-dimensional horror! Secondly, in the 'buddy' style maths chapter you'll get some
fear-mongering about gimbal lock, absolutely no analytical example of
where or how this happens, and a copy-and-paste function to "solve" the problem
without thinking about it.
Totally Backwards Gyroscope Videos
The go-to explanation of "gimbal lock" is a crudely-constructed 3d scene of
3 gimbals rotating with a miniature aeroplane in the middle of them. At some
point the narrator will make 2 of the gimbals line up, and then the aeroplane
can only pitch and roll, and the "yaw" gimbal also pitches, and it can no longer
yaw. This is ignorant in so many different dimensions!
- This is not how a gyroscope works
- The gimbals are not locking
- The axes were never clean local pitch/yaw/roll because they are in a hierarchy
- The aircraft should be on the outside of the gyroscope - they are missing a whole extra orientation
The primary confusion is that the narrator has tricked themselves into thinking
that their Z * Y * X combination of matrices are the same as a local
yaw/pitch/roll, except that it doesn't work in certain conditions. Wrong. If you
build one yourself, you'll discover that actually the axes are still global
X, Y, and Z. The local axes are never respected. All they've done is build a
parent-child relationship with the rotation matrices:
Only the bottom-level rotation is local to the miniature aeroplane. It's the
same as a skinned character animation where the ankle bone has its own local
orientation, but it also inherits the knee, and the knee inherits the hip. If
the hip rotates 45 degrees around Z then the knee around Y is going to give you
something half-way between a roll and a yaw. The 3d "gimbals" drawn here are a
bunch of hokum. I made one, to try it out:
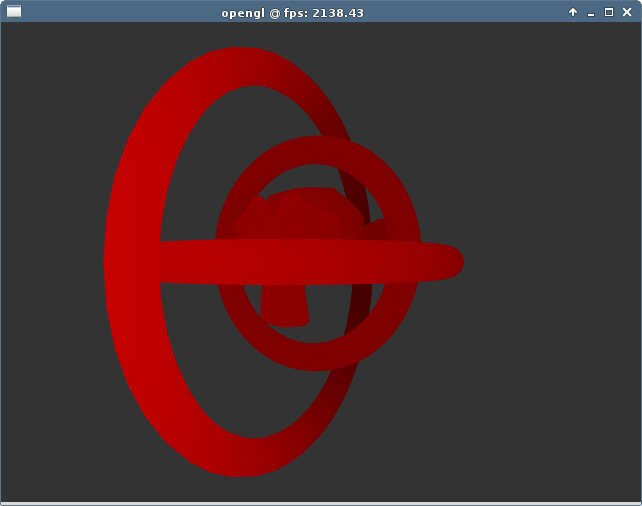 This kind of "gimbal lock" demo is rubbish: the problem is actually
that the rotations are in a hierarchy of rotations around global axes - they
were never around local axes to begin with. Gyroscopes don't work like this in
the real world - they do the opposite.
This kind of "gimbal lock" demo is rubbish: the problem is actually
that the rotations are in a hierarchy of rotations around global axes - they
were never around local axes to begin with. Gyroscopes don't work like this in
the real world - they do the opposite.
Yeah, that's not how a gyroscope works. First of all - the aircraft or ship is
on the outside of the gimbals, not in the middle, obviously. It has its own
3d orientation, independent of all 3 gimbals. The object
in the centre of the gimbals - usually a flywheel, but it can be a billiards
table or a pot in a ship's galley - is supposed to always stay facing the exact
same way. Whenever the aircraft rolls or pitches or yaws there is an axis that
can move to adjust, so that the billiards table isn't upset.
Now, in a real gyroscope, the ship might turn exactly 90 degrees which makes two
of the gimbals line up. That might upset the billiard balls because you lose an
axis entirely. This is easily solved by adding a fourth gimbal. We can't do that
with the rotation matrices. Our rotations are also no longer pitch/yaw/roll as
soon as the parent 'gimbals' are not perpendicular i.e. right away, not just when
just they line up to 90 degrees. So the analogy is wrong, as well as the
understanding of the problem.
Authors and narrators will blame Euler and gimbal lock...um no...you've just
misunderstood what you're doing. These matrix rotations are all correct, but
they are around global axes. The problem here is actually that what you
really want is 3 rotations around arbitrary axes which we will make
perpendicular to the object's current facing orientation. You can find functions
to create a rotation matrix about an arbitrary line (axis). I think it's very
unlikely that you've used a variant of this that is subject to an incomplete
domain, and really does undefined or locked orientations. By far the most
elegant way to compute this is with Hamilton's 4d quaternions. The fourth
dimension is used to resolve the 3d rotation very neatly.
Mmm
Why is this whole topic so badly explained and mis-informative? Are the maths
really that hard or 'scary'? Are the hard-core mathematicians really hiding from
explaining the problem properly? Is Hamilton rolling in his grave or pitching?
