Morph Target Animation / Quaternions
Dr Anton Gerdelan gerdela@scss.tcd.ie

About Me Working on smart buildings EU project with WebGL visualisation Lectured in Karlskrona, Sweden. 3d programming, games, visualisation Did most of PhD with GV2. Vehicle simulation, AI, graphics. Have a sort of blog about WebGL project and 3d stuff https://antongerdelan.net/

Morph Target Animation

Alternative to skinning/skeletal animation Good for detailed, "squishy" animations like faces, explosions, voluminous liquids, transformers... Can be hooked up with lip sync etc. "ah" "oh" "bee" etc. Technical artist creates copies of mesh in several "target" poses Our code blends smoothly between targets via linear interpolation Can blend final pose from several targets; neutral, happy, sad, eyes left, eyebrows...

image source: "Shape Keys", wiki.blender.org

Here's One That I Prepared Earlier

• Demos in WebGL:
  • Door https://antongerdelan.net/blog/morphtargets/
  • Face and Shaders https://antongerdelan.net/blog/editshaders/
• I used a free mesh from Turbosquid and exported it to several meshes.
• Vertices must be in same order in all targets or they will be mixed up during interpolation.
• Instead of using several meshes, we could store 1 mesh, and export a morph map texture for each pose.
  • Each texel rgb gives the scaled offset xyz of a vertex.
  • 512x512 supports ~260,000 vertices.
  • Sample textures in a vertex shader and interpolate as normal.

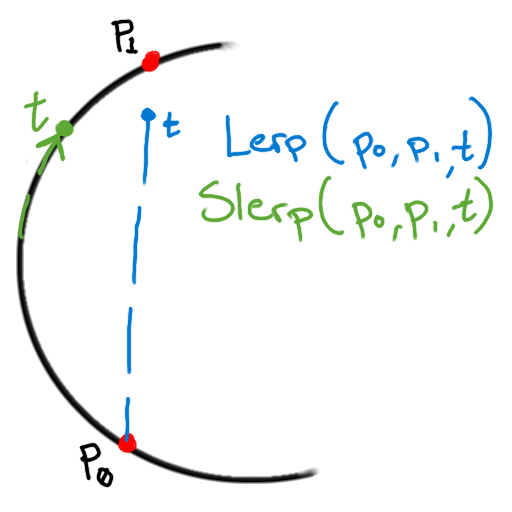
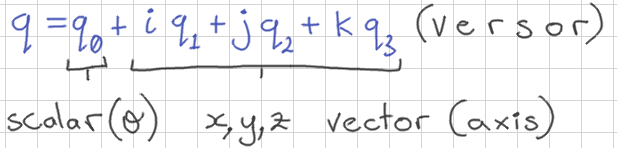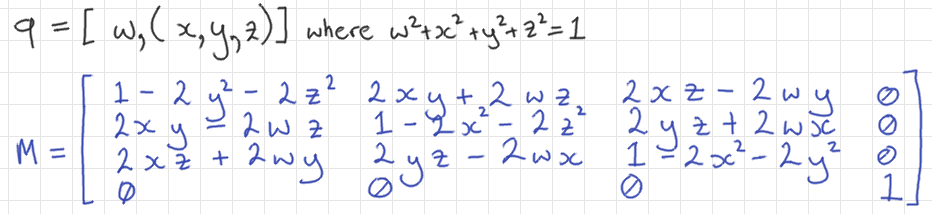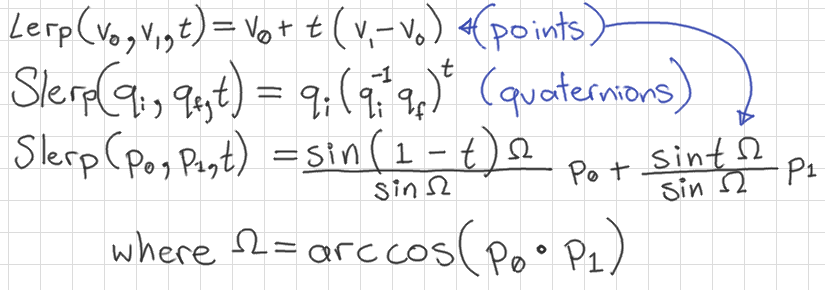Interpolation of Targets

• Each target has a weight of value 0 to 1
• Set position of each vertex with interpolation function. Do this each frame of rendering.
• If using shaders, put this function in vertex shader.
• For smooth animations, remember to multiply change in each weight by elapsed time

// assume we have set weights for happy and sad faces and have meshes
// work out how much of "neutral" pose to show
float w_neutral = 1.0 - w_happy - w_sad;
clamp (w_neutral, 0.0, 1.0);

// get each weight as a factor of total of weights
float w_sum = w_happy + w_sad + w_neutral;
float happy_factor = w_happy / w_sum;
float sad_factor = w_sad / w_sum;
float neutral_factor = w_neutral / w_sum;

// work out final position by doing weighted average of each target
vec3 mixed_xyz = mix (default_pos, happy_pos, happy_factor);
mixed_xyz = mix (mixed_xyz, sad_pos, sad_factor);

Quick Intro to Quaternions

Very hard to get a simple explanation ... until now Contriving a rotation from Rz * Ry * Rx matrices is cumbersome (order is important) some representations can have issues at extreme angles 1843. Enter: William Rowan Hamilton. Brougham Bridge (Royal Canal). Extension of complex numbers that gives us an elegant way of representing 3d rotations Can represent rotation between any 2 poses with 1 quaternion Some nice methods for interpolating. Think skeleton hierarchy or IK

Studied at Trinity

Rotation Quaternion

• A quaternion used for rotation is called a versor
• Predates vector calculus - so notation looks strange:
  
• Note - this is just 4 input numbers
• Most 3d maths libraries have quaternion functions; WildMagic, D3DX, GLM, Ogre3D ... etc.
• If you want to use a library, then use it something like:
  • create quat (angle, x, y, z); this creates a versor which is used for calculations
  • interpolate between key-frames q = slerp (q1, q2, t); rotation is in-between q1 (when t = 0) and q2 (when t =1)
  • produce a final rotation matrix mat4 R = q.get_matrix ();
  • model/world matrix created as normal e.g. mat4 M = S * T * R;
• We will briefly look at the maths behind these main functions...

Step 1: Build a Versor

• We know the components of our quaternion but we can't use it in equations yet
• A versor is the expression of the rotation in a 4d rotation vector
• A little bit like making a rotation matrix. Inputs: angle, axis
• Now we can do various maths operations with our quaternion

When Ready: Quaternion to Matrix

• Double-check that quaternion is still normalised first (floating point errors)
  
• Note: w,x,y,z here are the versor components q0,q1,q2,q3; not the original input axis and angle
• Now we can use it to rotate vectors
• Q. What does the transposed matrix look like?
• Q. How can we rotate around a point?

Re-normalise Quaternion

• May need to re-normalise before output
• Almost the same as vector normalisation. Component-wise
• Only compute sqrt if interior sum does not add to 1

Combine Rotations with Quaternion Multiplication

• Q' = Q1 * Q2
  
• Means "rotate Q2 first, then rotate Q1". Non-commutative
• But when animating we want to interpolate a rotation part-way between key-frames...

Interpolation with LERP and SLERP

• Animations key-frames have position, scale, rotation keys.
• Time between key-frames is 0-1.
  • Interpolate between scale, positions with LERP
  • Interpolate between rotations with SLERP
• Slerp goes shortest direction, circular arc (uniform velocity)
• .: Slerping wheels to rotate them can result in crazy animations

Issues with Skinning (Forward and Inverse Kinematics)